Сторінка
2

Лінійні неоднорідні системи

Нехай маємо систему

і - загальний розв’язок однорідної системи. Розв’язок неоднорідної будемо шукати в такому ж вигляді, але вважати не сталими, а невідомими функціями, тобто і ,чи в матричній формі

,

де -фундаментальна матриця розв’язків, - вектор з невідомих функцій. Підставивши в систему, одержимо

,

чи

.

Оскільки- фундаментальна матриця, тобто матриця складена з розв’язків, то

.

і залишається система рівнянь .

Розписавши покоординатно, одержимо

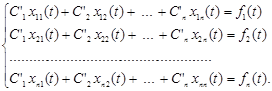
Оскільки визначником системи є визначник Вронського і він не дорівнює нулю, то система має єдиний розв’язок і функції визначаються в такий спосіб

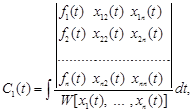
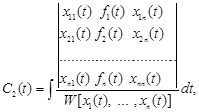
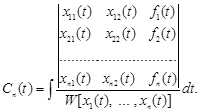
Звідси частинний розв’язок неоднорідної системи має вигляд

.

Для лінійної неоднорідної системи на площині

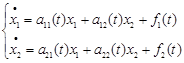
метод варіації довільної сталої реалізується таким чином.

Нехай

.

Фундаментальна матриця розв’язків однорідної системи. Тоді частинний розв’язок неоднорідної шукається у вигляді

Звідси

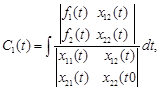
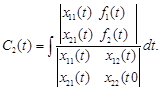
І загальний розв’язок має вигляд

, ,

де - довільні сталі.

4. Метод невизначених коефіцієнтів

Якщо система лінійних диференціальних рівнянь з сталими коефіцієнтами, а векторна функція спеціального виду, то частинний розв’язок можна знайти методом невизначених коефіцієнтів. Доведення існування частинного розв’язку зазначеного виду аналогічно доведенню для лінійних рівнянь вищих порядків.

1) Нехай кожна з компонент вектора є многочленом степеня не більш ніж , тобто

.

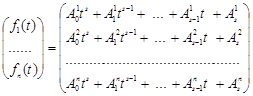а) Якщо характеристичне рівняння не має нульового кореня, тобто , , то частинний розв’язок шукається в такому ж вигляді, тобто

.

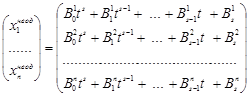б) Якщо характеристичне рівняння має нульовий корінь кратності , тобто , те частинний розв’язок шукається у вигляді многочлена степеня , тобто

.

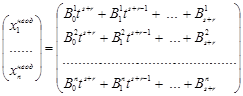Причому перші - коефіцієнти , , знаходяться точно, а інші з точністю до сталих інтегрування , що входять у загальний розв’язок однорідних систем.

2) Нехай має вид

.

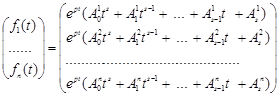а) Якщо характеристичне рівняння не має коренем значення , тобто , , то частинний розв’язок шукається в такому ж вигляді, тобто

.

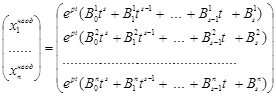б) Якщо є коренем характеристичного рівняння кратності , тобто, то частинний розв’язок шукається у вигляді