Сторінка
2

Зведення визначників до визначника Вандермонда

Далі, з четвертого стовпчика визначника віднімемо третій і т.д. Нарешті, з останнього n-го стовпчика віднімаємо (n-1)-й стовпчик. Одержуємо визначник Вандермонда:

D =.

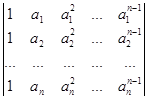Таким чином,

D =.

Задачі для самостійного розв’язування.

Обчислити визначник методом зведення до визначника Вандермонда

1.

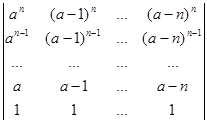
2.

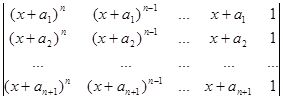
3.

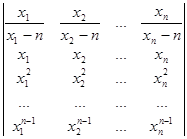
4.

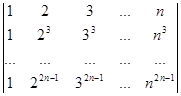
5.

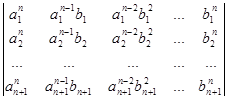
6.

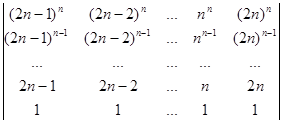
Список літератури

1. Курош А.Г. Курс высшей алгебры. – М., 1965.

2. Проскуряков И.В. Сборник задач по линейной алгебре. – М., 1984.

3. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М., 1977.