Сторінка
3

Розклад функцій в степеневий ряд. Достатні умовирозкладу в ряд Тейлора. Застосування степеневих рядів до наближеного обчислення

.

На основі теореми про інтегрування степеневих рядів одержимо при :

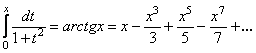. (13.61)

Аналогічно, підставляючи в ряд (2.46) замість вираз одержимо ряд

.

Інтегруючи даний ряд, будемо мати

. (13.62)

Цей ряд збігається в інтервалі . Можна було б довести, що ряд збігається при і що для цих значень сума ряду також дорівнює Тоді, поклавши в ряд (13.62) одержимо формулу для обчислення числа :

.

3. Розклад в степеневий ряд функції

Інтегруючи рівність (13.59) в межах від до (при ), одержимо:

(13.63)

Ця рівність справедлива на інтервалі

Замінюючи в формулі (13.63) на , одержимо ряд

, (13.64)

який збігається на інтервалі

За допомогою рядів (13.63) і (13.64) можна обчислювати логарифми чисел. що містяться між нулем та одиницею. Виведемо формулу для обчислення натуральних логарифмів довільних цілих чисел.

Оскільки два збіжних ряди можна почленно віднімати, то, віднімаючи від рівності (13.63) почленно рівність (13.64), отримаємо:

.

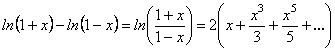Покладемо тоді При довільному натуральному маємо а тому

,

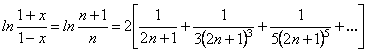звідки

.

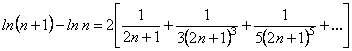(13.65)

13.14. Обчислення означених інтегралів за допомогою рядів

Розглядаючи інтеграли, було відмічено, що існують означені інтеграли, котрі, як функції верхньої границі, не виражаються через елементарні функції в скінченому вигляді. Такі інтеграли інколи буває зручно обчислювати за допомогою рядів.

Розглянемо декілька прикладів.

1. Обчислити

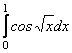
з точністю до

Використаємо ряд (2.41) для Тоді, замінюючи на одержимо

.

Цей ряд рівномірно збігається на всій числовій осі, тому його можна почленно інтегрувати на довільному проміжку. Інтегруючи даний ряд, одержимо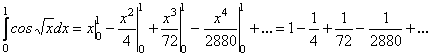Це знакочергуючий ряд. Тому, з точністю до , маємо

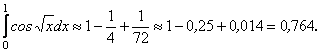
2. Обчислити інтеграл

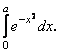
Тут первісна не є елементарною функцією. Для обчислення цього інтеграла скористаємося рядом (2.42), замінивши на :

.

Інтегруючи обидві частини рівності в межах від до , одержимо:

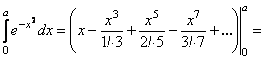
За допомогою цієї рівності можна при довільному обчислити даний інтеграл з довільною точністю.

3. Обчислити з точністю до 0.0001 , де

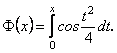
Замінюючи в ряді (13.55) на , одержимо

Інтегруючи почленно в межах від до будемо мати