Сторінка
3

Диференціальні рівняння першого порядку (з відокремлюваними змінними, однорідні, лінійні, Бернуллі)

або .

Зауваження. До однорідних рівнянь зводяться диференціальні рівняння вигляду

(12.12)

1. У разі, коли , слід виконати заміну змінних, де і - сталі, підібрані таким чином, щоб рівняння (12.12) перетворилося на однорідне рівняння вигляду

.

Оскільки та ,

сталі і слід підібрати так, щоб виконувались рівняння

Ця система має єдиний розв’язок (згідно з умовою ).

2. Якщо , то , оскільки , та . В цьому разі рівняння (12.12) подамо у вигляді

. (12.13)

Якщо в цьому рівнянні виконати заміну змінної за формулою , то рівняння (12.13) перетвориться у диференціальне рівняння з відокремлюваними змінними. Справді, маємо і , отже, .

Перейшовши до нової змінної у рівнянні (12.13), одержимо рівняння

,

у якому змінні легко відокремлюються.

Приклад 4. Розв’язати рівняння

.

Р о з в ‘ я з о к. Це - диференціальне рівняння вигляду (12.13). Перевіримо, чи виконується для нього нерівність . Отже, в цьому рівнянні слід виконати заміну змінних та за формулами . Підставимо нові змінні у вихідне рівняння:

.

Для визначення і отримаємо алгебраїчну систему двох лінійних рівнянь

головний визначник якої дорівнює і, отже, система має єдиний розв’язок:, . Це дозволяє виконати заміну змінних і: ,

в результаті якої отримуємо однорідне рівняння . Виконаємо в цьому рівнянні заміну змінної за формулою . Маємо .

Відокремлюємо змінні та :

.

Загальний інтеграл цього рівняння має вигляд

або

.

Враховуючи виконані заміни змінних, маємо:

.

Отже, загальний інтеграл вихідного рівняння

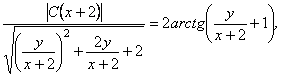
або, після спрощень,

.

12.4. Лінійні диференціальні рівняння першого порядку

Лінійними диференціальними рівняннями першого порядку називається рівняння, лінійне відносно невідомої функції та її похідної:

(12.14)

де - задані неперервні функції від .

Якщо, зокрема, , то рівняння

(12.15)

називається лінійним однорідним (або без правої частини), а рівняння (12.14), в якому - неоднорідним.

Однорідне рівняння (12.15) – це диференціальне рівняння з відокремлюваними змінними. Відокремлюємо змінні:

.

Загальний інтеграл рівняння

,

а загальний розв’язок однорідного рівняння (12.15)

(12.16)

Щоб відшукати загальний розв’язок рівняння (12.14), використаємо так званий метод варіації довільної сталої Лагранжа. Суть його полягає в тому, що розв’язок рівняння (12.14) шукатимемо у вигляді, аналогічному (12.16), але вважатимемо у цій формулі не сталою, а невідомою функцією від :

(12.17)