Сторінка
2
Кут ![]() водночас є кутом між віссю
водночас є кутом між віссю ![]() і перпендикуляром до площини (11.26). Тому на основі рівняння (11.26) і формули аналітичної геометрії маємо:
і перпендикуляром до площини (11.26). Тому на основі рівняння (11.26) і формули аналітичної геометрії маємо:
 .
.
Тоді
![]() .
.
Підставляючи цей вираз у формулу (11.27), дістанемо (зауваживши при цьому, що при
![]() ):
):

![]() .
.
Границя, яка стоїть у правій частині за означенням є подвійним інтегралом, тобто
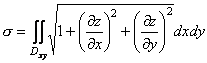 . (11.28)
. (11.28)
Це і є формула, за якою обчислюється площа поверхні ![]() .
.
Якщо рівняння поверхні задано у вигляді ![]() або
або
![]() , то відповідні формули для обчислення площі поверхні матимуть вигляд
, то відповідні формули для обчислення площі поверхні матимуть вигляд
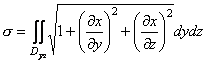 ,
,
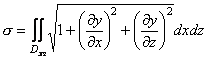 ,
,
де ![]() - області відповідно на площинах
- області відповідно на площинах ![]() і
і ![]() , в які проектується ця поверхня.
, в які проектується ця поверхня.
|
|
Рис.11.15
![]() що вирізається циліндром
що вирізається циліндром ![]()
Р о з в ‘ я з о к. Дана поверхня – параболоїд (рис.11.15). Обчислимо частинні похідні: ![]() Область інтегрування
Область інтегрування ![]() круг з радіусом, що дорівнює 1. Тоді за формулою (11.28) маємо, перейшовши в подвійному інтегралі до полярних координат:
круг з радіусом, що дорівнює 1. Тоді за формулою (11.28) маємо, перейшовши в подвійному інтегралі до полярних координат:
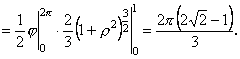
1 2
Інші реферати на тему «Математика»:
Загальний розв'язок задачі термінального керування і спостереження
Задачі геометричного і фізичного характеру, що приводять до диференціальних рівнянь
Задачі геометричного і фізичного змісту, що приводить до поняття подвійного інтеграла
Послідовності випадкових величин. Граничні теореми
Лінійні диференціальні рівняння вищих порядків