Сторінка
2
(9.10)
Формула (9.10) називається формулою парабол або Сімпсона. Доведено, що похибка обчислень 
за формулою Сімпсона є такою:
(9.11)
Проте цією оцінкою похибки можна користуватись, якщо 
є хоча б чотири рази диференційованою. Але якщо навіть чотири рази диференційована, то часто оцінка четвертої похідної 
може виявитись досить важкою. Тому на практиці часто користуються таким методом: обчислюють інтеграл, розділяючи інтервал, визначений границями інтегрування, один раз на 
рівних частин, а другий раз на 
частин. Якщо одержані двоє значень інтеграла мало відрізняються, то результат можна вважати прийнятним. Порівнюючи їх можна оцінити і точність обчислень.
Приклад. Обчислити з точністю до 0,001 інтеграл
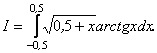
Р о з в ’ я з о к.За формулою (9.10) маємо:
при 
при 
|
|
|
|
|
|
| ||||
|
|
-0,5 |
0,0000 |
|
-0,5 |
0,00000 |
|
0,05 |
0,0371 | |
|
|
-0,4 |
-0,1203 |
|
-0,45 |
-0,0946 |
|
0,10 |
0,0772 | |
|
|
-0,3 |
-0,1303 |
|
-0,40 |
-0,1203 |
|
0,15 |
0,1200 | |
|
|
-0,2 |
-0,1081 |
|
-0,35 |
-0,1304 |
|
0,20 |
0,1652 | |
|
|
-0,1 |
-0,630 |
|
-0,30 |
-0,1303 |
|
0,25 |
0,2122 | |
|
|
0 |
0,0000 |
|
-0,25 |
-0,1204 |
|
0,30 |
0,2607 | |
|
|
0,1 |
0,0772 |
|
-0,20 |
-0,1081 |
|
0,35 |
0,3103 | |
|
|
0,2 |
0,1652 |
|
-0,15 |
-0,0881 |
|
0,40 |
0,3610 | |
|
|
0,3 |
0,2607 |
|
-0,10 |
-0,0630 |
|
0,45 |
0,4121 | |
|
|
0,4 |
0,36098 |
|
-0,05 |
-0,0335 |
|
0,50 |
0,4637 | |
|
|
0,5 |
0,46365 |
|
0,00 |
0,0000 |
Завантажити рефератІнші реферати на тему «Математика»:
Числові ряди. Збіжність і розбіжність. Сума ряду. Дії над збіжними рядами
Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних
Диференціальні рівняння вищих порядків
Основні правила диференціювання. Таблиця похідних
Лінійна однорідна система з постійними коефіцієнтами. Застосування теорії диференціальних рівнянь в економіці