Сторінка
2

Умовний екстремум. Метод множників Лагранжа. Метод найменших квадратів

Складаємо функцію Лагранжа

і прирівнюємо до нуля її частинні похідні:

, ,

, .

Звідси знаходимо . Точка є критичною точкою функції . Оскільки поставлена задача має певний розв’язок, а критична точка лише одна, то в цій критичній точці буде екстремум.

Шуканий паралелепіпед – куб із стороною .

2. Знаходження функції на основі експериментальних даних

за методом найменших квадратів

У різних областях людської діяльності широке розповсюдження мають формули, одержані на основі обробки спостережень або експериментів. Такі формули називаються емпіричними.

Нехай на основі експерименту потрібно встановити функціональну залежність величини від величини : .

В результаті одержано значень функції при відповідних значеннях аргументів і результати записані так:

Вид функції встановлюється або із теоретичних міркувань, або на основі аналізу графіка функції . Для цього слід побудувати в прямокутній декартовій системі координат точки, відповідні експериментальним значенням. Ці точки в дальшому будемо називати експериментальними. Якщо експериментальні точки розміщені на координатній площині так, як зображено на рис. 6.15, то доречно будувати залежність від у вигляді лінійної функції . Якщо експериментальні точки розміщені так, як показано на рис. 6.16, то функцію будемо шукати у вигляді .

При вибраному вигляді функції залишається добрати параметри так, щоб вони якнайкраще і описували

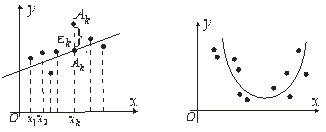
Рис.6.13 Рис.6.14

розглядуваний процес. Найпоширенішим методом розв’язання даної задачі є метод розв’язання даної задачі є метод найменших квадратів.

Нехай експериментальні точки групуються навколо прямої (див. рис. 6.13). Тоді

(6.97)

де і - параметри, які потрібно знайти.

Розглянемо експериментальну точку і точку з такою самою абсцисою, але яка лежить на прямій. Її координати . Різницю ординат цих точок

, (6.98)

що являє собою відхилення точки від прямої , назвемо похибкою.

Доберемо параметри і так, щоб сума квадратів похибок

(6.99)

була найменшою.

Підставимо в (6.99) вирази помилок (6.98), одержимо

(6.100)

Тут і відомі величини, а і - невідомі, які потрібно знайти. Для того щоб функція мала найменше значення, необхідно

виконати умови:

або

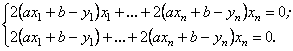
Перегрупувавши члени, подамо цю систему у вигляді

або

(6.101)

Ця система рівнянь називається нормальною системою методу найменших квадратів. Розв’язавши її, знаходимо і і підставляємо в емпіричну формулу .

Нехай тепер експериментальні точки розміщені поблизу деякої параболи (див. рис. 6.14). Тоді

(6.102)

Для знаходження і використаємо метод найменших квадратів. Відхилення за ординатою експериментальних точок від відповідних точок параболи