Сторінка
3

Лінійне відображення лінійного простору і його матриця, афінне відображення

Для доведення досить виписати такі рівності:

Теорема 2. Якщо в лінійному просторі існує базис із векторів, то довільний інший базис в цьому просторі складається із того ж числа векторів.

Д о в е д е н н я. Нехай в лінійному просторі існує два базисі і причому Кожний з векторів базису розкладемо за векторами базису і складемо матрицю, стовпчиками якої будуть одержані координатні стовпчики. Кожний стовпчик має висоту а їх всього Тому матриця має розміри і ранг її не перевищує В силу теореми 2 п.4.1.3 стовпчики матриці лінійно залежні, а, значить, залежні і вектори Таким чином, наше припущення приводить до протиріччя. Теорема доведена.

Означення. Лінійний простір, в якому існує базис із векторів, називається вимірним, а число розмірністю простору. Розмірність простору будемо вказувати нижнім індексом, наприклад - вимірний лінійний простір.

В нульовому просторі немає базису, оскільки система, що складається із одного нульового вектора, є лінійно залежною. Розмірність нульового простору дорівнює нулю.

Може виявитися, що яке б не було натуральне в просторі знайдеться лінійно незалежних векторів. Такий простір називається нескінченновимірним. Базису в ньому не існує.

Якщо в вимірному просторі задані два базиси і , то ми можемо розкласти кожний вектор базису за векторами базису :

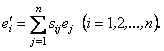(4.11)

Координати можна записати у вигляді квадратної матриці

Стовпчики матриці це координатні стовпчики векторів за базисом Тому стовпчики матриці лінійно незалежні і

Матриця, ий стовпчик якого є координатний стовпчик вектора за базисом називається матрицею переходу від базису до базису

Рівність (4.11) можна записати в матричному вигляді

(4.12)

Перемножуючи рівність (4.12) на матрицю одержимо

Звідси випливає, що є матрицею переходу від базису до

Вияснимо, як зв’язані між собою координати одного і того ж вектора в двох базисах і Позначимо через і координатні стовпчики вектора в цих базисах. Це означає, що і звідки одержимо Якщо матриця переходу від базису до то і тоді або З останньої рівності одержимо:

(4.12)

4.3.3. Лінійні відображення і перетворення

Означення 1. Нехай і два лінійних простори. Відображенням простору в простір називається закон, за яким кожному вектору із співставляється єдиний вектор із . Ми будемо це записувати коротко так: Образ вектора позначається