Сторінка
4

Формування поняття функції в курсі середньої школи

Функція називається непарною, якщо для будь-якого х з області визначення функції виконується рівність .

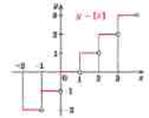
Рис. 1.1.8 Графік функції цілої частини аргументу

Область визначення цієї функції – множина всіх дійсних чисел, а область значень - множина всіх цілих чисел.

На рис. 1.1.9 наведено графік числової функції дробової частини аргументу , де – позначення дробової частини числа (за означенням

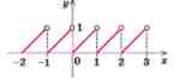
Рис. 1.1.9. Графік числової функції дробової частини аргументу

Одними з найбільш важливих властивостей функцій є їх зростаючий чи спадний характер. Функція є зростаючою на множині аргументів при умовах: якщо , то для всіх (при збільшені аргументу збільшується значення функції – рис. 1.1.10а).

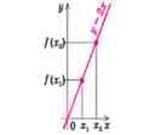
Рис. 1.1.10. Приклади графіків функцій

Функція є спадною на множині аргументів : якщо , то для всіх (при збільшені аргументу зменшується значення функції – рис. 1.1.10б).

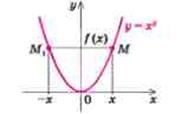
Рис. 1.1.11. Приклад графіка складеної зростаючої та спадної функції на окремих проміжках області визначення аргументів

Розглянемо детальніше приклади зростаючих та спадних функцій на ок-ремих проміжках визначення аргументів. Якщо на рис. 1.1.10. наведені приклади графіків тільки зростаючої а) та тільки спадаючої б) функцій, то на графіку рис. 1.1.11 бачимо, що на всій області визначення ця функції не є ні зростаючими, ні спадними. Але можна виділити проміжки області визначення, де ці функції зростають і де спадають. Так, на проміжку функції зростає а на проміжку – спадає.

Розглянемо властивості парності і непарності функцій, області визначен-ня яких симетричні відносно початку координат, тобто разом з кожним числом містять і число . Для таких функцій визначено поняття парності і непарності.

Функція називається парною (рис. 1.1.12а), якщо для будь-якого з її області визначення Якщо функція парна, то до її графіка разом з кожною точкою з координатами входить також і точка з координатами . Точки і розміщені симетрично відносно осі (рис. 1.1.12а) тому й графік парної функції розміщений симетрично відносно .

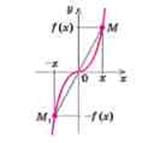
Рис. 1.1.12. Типові графіки парної

Функція називається непарною (рис. 1.1.12б), якщо для будь-якого з її області визначення

Якщо функція непарна, то до її графіка разом з кожною точкою з координатами входить також і точка з координатами . Точки і розміщені симетрично відносно початку координат (рис. 1.1.12б), тому й графік непарної функції розміщений симетрично відносно початку координат.

Наприклад, функція (тобто функція ) – парна, оскільки (рис. 1.1.13а). Графік парної функції симетричний відносно осі (рис. 1.1.13а).

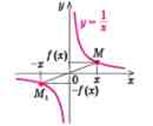
Рис. 1.1.13. Графіки парної функції та непарної функції

Функція (тобто функція ) – непарна оскільки (рис. 1.1.13б): Графік непарної функції симетричний відносно початку координат, тобто відносно точки (рис. 1.1.13б).