Сторінка
15

Методика навчання диференціальних рівнянь майбутніх вчителів математики в педагогічних університетах

.

1.3. Порівняємо частинні похідні. Так як , то рівняння є рівнянням в повних диференціалах.

20. Запишемо формулу загального інтеграла:

30. Виберемо формулу для відшукання функції :

40. Знайдемо функцію :

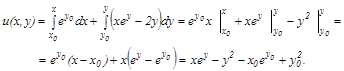
50. Запишемо загальний інтеграл рівняння:

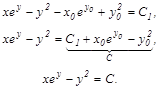
Приклад 3. Знайти загальний інтеграл диференціального рівняння

Відповідь:

Приклад 4. Серед рівнянь вказати те, яке є одночасно однорідним і в повних диференціалах:

а)

б)

в)

2. Інтегруючий множник

Нехай функції неперервні в області вигляду . Якщо для рівняння

(1)

умова не виконується в області , то це рівняння не буде рівнянням у повних диференціалах у цій області.

В цьому разі виникає питання, чи не можна підібрати функцію так, щоб після множення на неї рівняння (1) дістали рівняння

(1’)

в повних диференціалах. Така функція називається інтегруючим множником диференціального рівняння (1).

Щоб функція , неперервна в однов’язній області разом зі своїми частинними похідними і , була інтегруючим множником рівняння (1), необхідно і достатньо, щоб для всіх точок виконувалась рівність

,

тобто

. (2)

Рівність (2) містить невідому функцію під знаком частинних похідних, тобто (2) є диференціальне рівняння в частинних похідних. Його розв’язання є задачею складнішою, ніж розв’язання рівняння (1). Однак задача по знаходженню інтегруючого множника значно спрощується, коли відомо, що він залежить від однієї незамкненої змінної або .

Припустимо, що рівняння (1) має інтегруючий множник, залежний тільки від . В цьому разі рівняння (2) набере вигляду

,

або ,

звідки 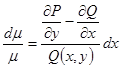. (3)

Оскільки є функцією однієї незалежної змінної , то вираз

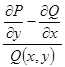(4)

не повинен залежати від . Позначивши його через і припускаючи, що - неперервна функція в інтервалі , з (3) дістанемо

і, таким чином,

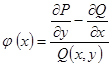, де . (5)

Покажемо, що коли вираз (4) справді не залежить від і є неперервною функцією від на інтервалі , то функція , задана рівністю (5), є інтегруючим множником рівняння (1).

Справді, для цього достатньо переконатись у справедливості рівності

(6)

для всіх точок . Маємо

,

,

тобто рівність (6) дійсно виконується в області .

В аналогічній спосіб можна показати, що коли вираз

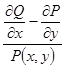
не залежить від і є неперервною в інтервалі , то рівняння (1) має інтегруючий множник, незалежний від , який знаходиться за формулою

.

Розглянемо питання про еквівалентність рівнянь (1) і (1’). Якщо є інтегруючий множник рівняння (1), то рівняння

(7)

є рівнянням в повних диференціалах, тобто існує функція , повний диференціал якої дорівнює лівій частині цього рівняння:

. (8)

Загальний інтеграл рівняння (7) має вигляд

.

З (8) дістанемо

(9)