Сторінка
4

Динамічні властивості нелінійних локалізованих мод у лінійних молекулярних ланцюжках

а в довгохвильовому наближенні sin (ka/2) » ka/2, звідки маємо . Фазова і групова швидкості у цьому випадку будуть сталі і дорівнюватимуть [3].

Бачимо, що акустичні фонони мають дисперсію звукових хвиль (достатньо порівняти з і повернутися до міркувань Частини І.

Оптичні фонони відрізняються від акустичних іншим законом дисперсії. Якщо для других у довгохвильовому наближенні , то перші задовільняють таке дисперсійне співвідношення:

де v0 – мінімальна фазова швидкість фонона. Її наявність і відрізняє оптичні фонони від акустичних, у яких фазова швидкість є сталою (в континуальному наближенні). Фазова швидкість оптичних фононів змінюється від v0 до нескінченості [6].

Дисперсійні співвідношення - вважатимемо означенням акустичних і оптичних фононів відповідно.

Рівняння, що описують поширення колективних збуджень із урахуванням взаємодії з акустичними фононами. Континуальна модель. Солітони як розв’язки нелінійного рівняння Шредінґера.

Рівняння, що описують поширення колективних збуджень із урахуванням взаємодії з акустичними фононами. Континуальна модель.

Раніше ми вже зазначали, що гамільтоніан системи, що описує поширення збуджень у молекулярному ланцюжку, складається із гамільтоніана квазічастинки, гамільтоніана фононів і гамільтоніана взаємодії між ними. У співвідношенні ми нехтуємо внутрішньомолекулярними коливаннями, і тоді загальний гамільтоніан матиме вигляд:

Як вже було зазначено, гамільтоніан акустичного фонона має вигляд . Гамільтоніан електрона має зміст суми кінетичної і потенційної енергії, він задається через хвильову функцію квазічастинки і має вигляд:

де E0 – початкова енергія електрона, – енергія резонансної взаємодії (a - стала ґратки, d – дипольний момент) [3][4].

Нарешті, гамільтоніан взаємодії має вигляд:

Склавши , і , матимемо вираз для загального гамільтоніана системи:

де введено позначення – енергія деформації ланцюжка.

Цей гамільтоніан задовільняє гамільтонові рівняння:

де – узагальнені координати, – узагальнені імпульси. Тоді ці рівняння набудуть вигляду:

Окрім того, поклавши q = un, p= pn, отримаємо другу систему рівнянь:

Підставимо вираз для гамільтоніана у друге рівняння і продифереціюємо по Yn*:

Це і буде перше шукане рівняння, що описує поширення квазічастинки (перші два члени правої частини) і взаємодії її з деформацією (третій член) [4].

Ліва і права частина цього рівняння мають розмірність енергії, і тому цілком очевидно, що перед нами закон збереження енергії квазічастинки. Рівняння для комплексно спряженої функції [перше з рівнянь ] є аналогічним до рівняння , але записаним у спряжених функціях, і тому його не розглядаємо. Зрозуміло, що одного рівняння для електрона недостатньо, потрібно ще рівняння для деформації. Його отримаємо, підставивши гамільтоніан у друге рівняння і замінивши pn = Mun. Після спрощення отримаємо друге шукане рівняння [4]:

Чисельне інтеґрування рівнянь - у роботах [4], [8] показало, що за певних умов в ланцюжку утворюються автолокалізовані стани квазічастинки, які було названо давидівськими солітонами[6]. Давидов показав це, користуючись довгохвильовою (континуальною) моделлю [3][7]. Як було зазначено раніше, у випадку довгих хвиль середовище можемо вважати суцільним і покласти

де . Підставивши це в наші рівняння, здобудемо:

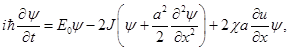
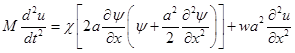
Під y і u ми розуміємо відповідні функції y(x,t) та u(x,t). Перетворимо перше рівняння системи:

Замінимо . Підставивши у це рівняння цю заміну і спростивши його, отримаємо остаточно: