Сторінка
1
Корелатний метод
Розглянемо полігонометричний хід А, 1, 2, ., n, С, в якому виміряні кути 
, сторони 
, відомі координати пунктів А і С, та вихідні дирекційні кути 
та 
(рис. 3.17).
В даному ході виникають три умовні рівняння: дирекцій них кутів та координат (абсцис та ординат).
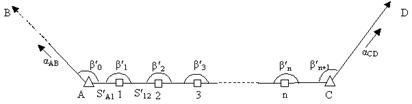
Рис. 3.17 Окремий полігонометричний хід
3.8.1.1. Умовне рівняння дирекційних кутів
Маємо
|
|
(3.87) |
, де 
— найімовірніші значення виміряних кутів.
Підставивши в формулу (3.87) виміряні значення кутів отримаємо
|
|
(3.88) |
. Значення частинних похідних
|
|
(3.89) |
. З врахуванням (3.89) рівняння поправок для дирекцій них кутів буде
|
|
(3.90) |
. 3.8.1.2. Координатні умовні рівняння
Запишемо рівняння зв’язку для абсцис. Маємо
|
|
(3.91) |
, або з врахуванням результатів вимірів
|
|
(3.92) |
, де
|
|
(3.93) |
. Зауважимо, що
|
|
(3.94) |
. Знайдемо частинні похідні 
та 
. Маємо
|
|
(3.95) |
. Таким чином, з врахуванням (3.95) умовне рівняння абсцис має вигляд
|
|
(3.96) |
. Або позначивши 
, в скороченому записі отримаємо
|
|
(3.97) |
. Для ординат рівняння зв’язку має вигляд.
|
|
(3.98) |
. Або з врахуванням виміряних величин
|
|
(3.99) |
, де
|
|
(3.100) |
. 
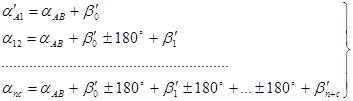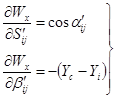Завантажити реферат