Сторінка
1

Хвильовий опір хвильовода

Для Т – хвилі: (для вакууму). Для ТЕ, ТМ хвиль введення хвильового опору не є однозначною задачею, бо існує кілька компонент. Домовились відносити опір до поперечної компоненти: .

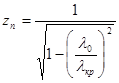
Електродинамічні потенціали

Векторний і скалярний потенціали вводяться наступним чином: ; . У першому рівнянні, очевидно, можна задавати з точністю до . При цьому рівняння Максвела:

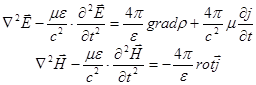
Тоді отримаємо рівняння для ЕД потенціалів:

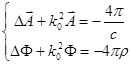
Рівняння для Т, ТЕ, ТМ хвиль різні. Щоб звести їх до одного виду, використовуючи потенціали , , де - електрична скалярна функція, - магнітна скалярна функція. Якщо для Т – хвилі завжди, то , а перетворюється в нуль завдяки . Рівняння для :

.

При цьому компоненти .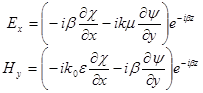

Інші компоненти можна отримати методом, який розглядався раніше. Для циліндричної СК: .

Круглий хвильовід.

Очевидно, будемо користуватися циліндричною СК :

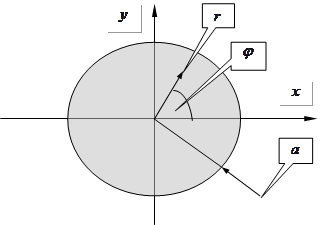Шукатимемо хвилю . Можна розв’язати , однак ми розв’яжемо рівняння для скалярних потенціалів: . З урахуванням вигляду оператора Лапласа у циліндричній системі координат одержимо: .

Використаємо метод відокремлення змінних:

;

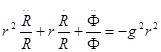. Звідки очевидно, що:

а) , тут - будь-який кут повороту, залежить лише від вибору координат (з’явився через симетрію задачі). Оберемо .

б) - ЛДР зі змінними коефіцієнтами, тому звичайним шляхом його розв’язувати неможливо; потрібно застосувати спеціальні функції. Приведемо рівняння до стандартного вигляду: заміною воно зводиться до рівняння Бесселя:

.

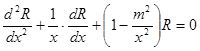Його розв’язками є циліндричні функції (функції Бесселя):

(*)

Функції Неймана , а тому очевидно, що , тому що поле при повинно бути скінченим. Таким чином, якщо в задачі існує точка , то розв’язок завжди береться у вигляді (*), де , тобто у вигляді функції Бесселя: .

Таким чином, , .

Скористаємося граничними умовами. Оскільки ; а ; то можна записати: . Отже, - це є умова для визначення . Корені цього рівняння аналітично не отримуються, але їх можна знайти чисельно: