Сторінка
1

Затухання у металі, скін – шар

ЕМХ як , для металу , тоді маємо . Оскільки , то . В металі хвиля затухає як . Глибина, на якій хвиля спадає в раз називається скін – шаром. . Для постійного поля .

Перехід хвилі з одного середовища в інше.

Розглянемо такий випадок: (див. Мал.)

Це – гранична задача електродинаміки.

Для її розв’язку необхідно:

1. Розв’язати рівняння Максвела у кожному середовищі.

2. Прирівняти розв’язки на границі.

3. З отриманих алгебраїчних рівнянь одержати всі характеристики ЕМП.

Спочатку обираємо повну систему рівнянь Максвела, однак оскільки обидва середовища – однорідні ізотропні, можна використати векторне рівняння Максвела: .

Межа – пряма, тому обираємо декартову СК: . У даних середовищах буде: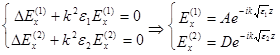

Нехай , тоді .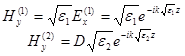

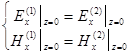Підставивши одержимо: 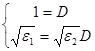- система несумісна. Ми не врахували те, що існує також відбита хвиля у середовищі (1):

. При відбитті трійка векторів залишається правою, тому напрямок вектора змінюється, тому у виразі для - мінус:

.

Підставивши одержимо:

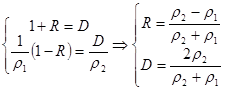
Таким чином, найбільша (повна) передача енергії в друге середовище при - коефіцієнт відбиття . По аналогії з електротехнікою величини називають опорами.