Сторінка
2
Якщо вузли ![]() вибрати з міркувань зручності (рівномірно розташованими
вибрати з міркувань зручності (рівномірно розташованими ![]() ,), а коефіцієнти
,), а коефіцієнти ![]() - з міркувань точності, то у випадку
- з міркувань точності, то у випадку ![]() отримаємо квадратурні формули Ньютона - Котеса.
отримаємо квадратурні формули Ньютона - Котеса.
Якщо вузли ![]() вибрати з міркувань точності, а коефіцієнти
вибрати з міркувань точності, а коефіцієнти ![]() - з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова.
- з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова.
Обгрунтування інтерполяційних квадратурних формул будується на наступних висновках .
Нехай на відрізку інтегрування якось зафіксовані різні між собою вузли ![]() , і будемо вибирати лише коефіцієнти
, і будемо вибирати лише коефіцієнти ![]() (
(![]() ) так, щоб формула (1.4) була якомога точнішою. Припускаємо,
) так, щоб формула (1.4) була якомога точнішою. Припускаємо, ![]() , тобто функія
, тобто функія ![]() і всі її похідні до
і всі її похідні до ![]() порядку включно є неперервними на відрізку
порядку включно є неперервними на відрізку ![]() . Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен
. Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен ![]() для функції
для функції ![]() . Будемо мати таку рівність
. Будемо мати таку рівність
![]() (1.5)
(1.5)
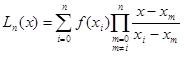 (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
Розглянемо тепер інтеграл від функції ![]()
![]()
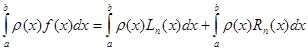 (1.9)
(1.9)
підставимо (1.6), (1.7), (1,8) до формули (1.9)
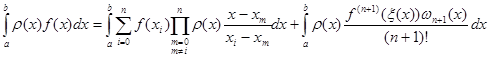 (1.10)
(1.10)
Якщо позначити
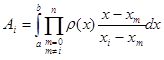 (1.11)
(1.11)
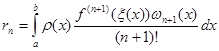 (1.12)
(1.12)
то інтеграл (1.10) можна переписати у вигляді
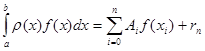 (1.13)
(1.13)
Відкинувши у (1.13) похибку ![]() , добудемо наближену формулу (1.4).
, добудемо наближену формулу (1.4).
Означення. Квадратурна формула (1.4) будемо називати інтерполяційною, якщо квадратурні коефіцієнти ![]() ,
,![]() визначаються формулами (1.11). Нагадаємо, що квадратурні вузли при цьому всі різні та всі розташовані на відрізку інтегрування, в усьому іншому вони довільні.
визначаються формулами (1.11). Нагадаємо, що квадратурні вузли при цьому всі різні та всі розташовані на відрізку інтегрування, в усьому іншому вони довільні.
Формула (1.12) визначає похибку інтерполяційної квадратурної формули. З похибки видно, що алгебраїчний степінь точності інтерполяційної квадратурної формули дорівнює ![]() . Збільшити степінь точності можна лише за рахунок вибору вузлів
. Збільшити степінь точності можна лише за рахунок вибору вузлів ![]() .
.
Квадратурні формули при сталій ваговій функції та з рівновіддаленими вузлами називають формулами Ньютона-Котеса у пам’ять того, що вперше вони в достатньому загальному вигляді були розглянуті Ньютоном, коефіцієнти вперше були добуті Котесом ![]() .
.
Кінечний відрізок інтегрування ![]() ділимо на
ділимо на ![]() рівних частин довжини
рівних частин довжини ![]() , точки ділення беремо за вузли інтерполяційної формули. Спростимо вигляд квадратурних коефіцієнтів
, точки ділення беремо за вузли інтерполяційної формули. Спростимо вигляд квадратурних коефіцієнтів ![]() ,
,![]() , які визначаються формулою (1.11), підставивши туди
, які визначаються формулою (1.11), підставивши туди
![]() ,
,![]() .
.
Крім того перейдемо до нової змінної інтегрування ![]() , де
, де ![]()
Для виконання всіх цих дій спочатку розглянемо добуток у формулі (1.11)
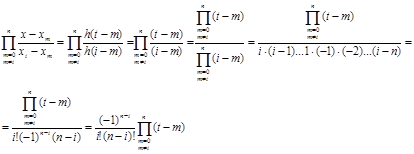 (1.14)
(1.14)
Підставимо добуток (1.14) до формули (1.11) та перейдемо до нової змінної, будемо мати
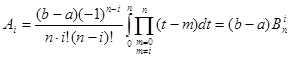 (1.15)
(1.15)
Де
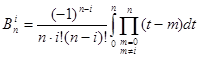 (1.16)
(1.16)
Квадратурна формула Ньютона-Котеса приймає вигляд
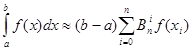 (1.17)
(1.17)
Алгебраїчна степінь точності формули (1.17) дорівнює ![]() . Коефіцієнти (1.16) називаються коефіцієнтами Котеса. Вони мають властивості:
. Коефіцієнти (1.16) називаються коефіцієнтами Котеса. Вони мають властивості:
![]() . Дійсно, підставимо до формули (1.17)
. Дійсно, підставимо до формули (1.17) ![]() , тоді
, тоді ![]() , при цьому наближена формула стає точною. Виконуємо інтегрування властивість доведена.
, при цьому наближена формула стає точною. Виконуємо інтегрування властивість доведена.
![]() , тобто рівновіддалені від кінців коефіцієнти формули Ньютона -Котеса є однаковими. Дійсно, маємо з формули (1.16)
, тобто рівновіддалені від кінців коефіцієнти формули Ньютона -Котеса є однаковими. Дійсно, маємо з формули (1.16)
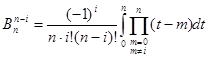
Зробимо заміну змінної інтегрування ![]() тоді
тоді
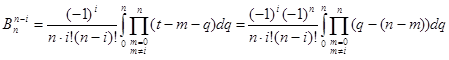
В добутку перейдемо до нового індексу ![]() і властивість доведена
і властивість доведена
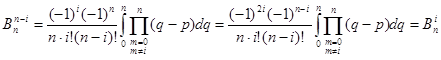
3. Коефіцієнти ![]() не залежать від довжини відрізка інтегрування та підінтегральної функції
не залежать від довжини відрізка інтегрування та підінтегральної функції![]() , тому вони можуть бути обчислені раз і назавжди
, тому вони можуть бути обчислені раз і назавжди
В залежності від вибраного параметра n отримана загальна форма квадратурних рівнянь розподіляється на випадки:
1) Коли ![]() , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула трапеції”;
, то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула трапеції”;
Інші реферати на тему «Педагогіка, виховання»:
Роль тренера в підготовці спортсмена
Використання сучасних технічних засобів в процесі вивчення іноземної мови
Формування умов інклюзії для розвитку дитини в закладах освіти
Літературні ігри на уроках читання як засіб літературного розвитку молодших школярів
Теоретичні основи виховання емоційно-позитивного ставлення до природи у дітей дошкільного віку
